线性代数作为数学的重要分支,在众多领域有着广泛应用。而maple软件为解决线性代数问题提供了强大且便捷的工具。
矩阵运算轻松实现
maple能快速进行矩阵的加、减、乘等基本运算。比如,定义两个矩阵a和b,只需简单输入指令,就能瞬间得出它们相加或相乘的结果。对于大规模矩阵运算,maple的高效性更是凸显,大大节省了手动计算的时间和精力。
行列式计算准确无误
计算矩阵的行列式是线性代数中的常见任务。使用maple,只需一行代码就能准确求出复杂矩阵的行列式值。无论是二阶、三阶矩阵,还是高阶矩阵,maple都能精准计算,避免了繁琐的展开式计算过程中可能出现的错误。
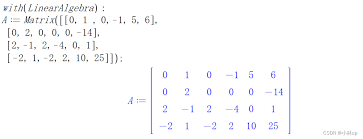
求逆矩阵快速便捷
求矩阵的逆在很多实际问题中至关重要。maple可以迅速求出可逆矩阵的逆矩阵。无需手动计算伴随矩阵和行列式的值再进行复杂的除法运算,maple一键操作,结果即刻呈现,极大地提高了工作效率。
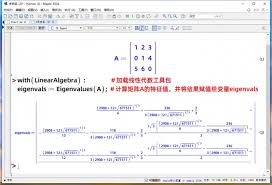
特征值与特征向量求解高效
maple能够高效地计算矩阵的特征值和特征向量。对于给定矩阵,通过简单指令就能得到其所有特征值,并相应地求出对应的特征向量。这对于分析矩阵的性质、解决线性变换等问题提供了有力支持。
线性方程组求解灵活多样
在解决线性方程组问题时,maple同样表现出色。它可以通过多种方法求解,如高斯消元法、lu分解法等。不仅能给出方程组的解,还能详细展示求解过程,帮助用户深入理解线性方程组的求解原理。
总之,maple在解决线性代数问题方面功能强大、操作简便。无论是学术研究还是实际应用,它都能成为我们解决线性代数难题的得力助手,让复杂的线性代数问题迎刃而解。

魅族手机以其独特的设计和出色的性能受到不少用户喜爱,但也有部分用户希望能体验鸿蒙系统。然而,目前魅族手机官方并没有推出原生适配鸿蒙系统的方案。从技术层面来说,不同手机厂商的系统底层架构存在差异。鸿蒙系统基于华为自主研发的微内核,而魅族手机原本使用的是基于安卓的

在安卓手机上观看抖音时,想要获得更清晰的画质体验,掌握画质增强的开启方法以及一些观看清晰度提升技巧至关重要。下面就为大家详细介绍。安卓手机画质增强开启方法不同品牌和型号的安卓手机,开启画质增强的方式略有不同。一般来说,可以在手机的“设置”中查找相关选项。比如,
在抖音这个充满活力与互动的社交平台上,有时候我们可能希望在享受精彩内容的同时,避免被过多的好友消息打扰。那么,抖音好友消息免打扰该在哪里开启呢?下面就为大家详细介绍。打开抖音应用,进入到主界面。然后,点击界面右下角的“我”选项。进入个人页面后,再点击右上角的三
在qq音乐评论区发表情包,能为你的评论增添别样的色彩,让交流更加生动有趣。下面就来详细介绍一下具体的方法。首先,要准备好你想要发送的表情包。可以从手机相册中挑选那些可爱、搞怪或者能准确表达你此刻心情的表情包。当然,也可以提前在网络上下载一些热门的表情包,以便随
在全民k歌的世界里,许多用户都对能否看到访客这一功能充满好奇。全民k歌能看到访客吗?这是一个备受关注的问题。对于很多热衷于在全民k歌展示自己歌声的人来说,了解谁访问了自己的作品页面,似乎能带来一种别样的满足感。有人觉得,如果能看到访客,就能知道自己的歌声吸引了
方式一:在个人评论页面查看打开喜马拉雅app,点击界面右下角的“账号”图标。进入个人账号页面后,找到“我的评论”选项并点击。这里会清晰地展示你在平台上发布的所有评论,按照时间顺序排列,最早的评论排在最上方。你可以轻松浏览每一条评论的具体内容、发布时间以及所在的